The term Mathematical Optimization (MO) isn’t sexy or sci-fi at all, and unlike the term “AI” is more likely to give you nightmares about highschool algebra rather than dreams about sentient robots. However, we do like the sound of making things “optimal”, so let’s dig a little deeper.
This is the second in a series of 3 blog posts that serialize a white paper on the use of Artificial Intelligence and Mathematical Optimization in business and public sector organizations.
While the white paper goes a little deeper, the blog posts follow the same structure to summarize:
- where Machine Learning (ML) as a generalization of AI has found its place in process automation and decision support, and reasons why many potential applications have been slower to see value from ML
- what Mathematical Optimization (MO) does in comparison with ML
- how MO and ML can work together in hybrid solutions that offer more value than the sum of their parts.
In the last blog post we describe some fundamental characteristics of Machine Learning as needed to highlight some of the challenges it faces.
In this blog post we describe some fundamental aspects of Mathematical Optimization as needed to highlight differences and similarities with Machine Learning and the challenges still faced by MO.
Making things happen
To “make things optimal”, MO provides the decisions that are known to lead to an optimal situation (e.g. minimal cost or maximal revenue). As this sounds too good to be true, we need to be aware of the requirement that MO needs to know directly how the decisions affect the thing (cost or revenue) that we are optimizing. Knowing this relationship can seem like something of a luxury, but the requirement is satisfied in many behind-the-scenes processes.
When MO is applicable it is powerful because, while ML provides predictions on which to base decisions, MO provides the decisions themselves allowing us to act directly. For example, an MO solver looking for the best allocation of different ticket types to all seats in a theater audience, evaluates the quality of all possible combinations of ticket and seat – all possible “decisions” of which there may be billions. The result of optimization is then the best seat allocation, i.e. a decision.
The value of MO is shown in the “Value Complexity Ramp of Analytics” (FIGURE 3), wherein MO is an example of “prescriptive” analytics, ML is “predictive” and, for completion, Business Intelligence (BI) products such as reports and ad-hoc studies are “descriptive”.
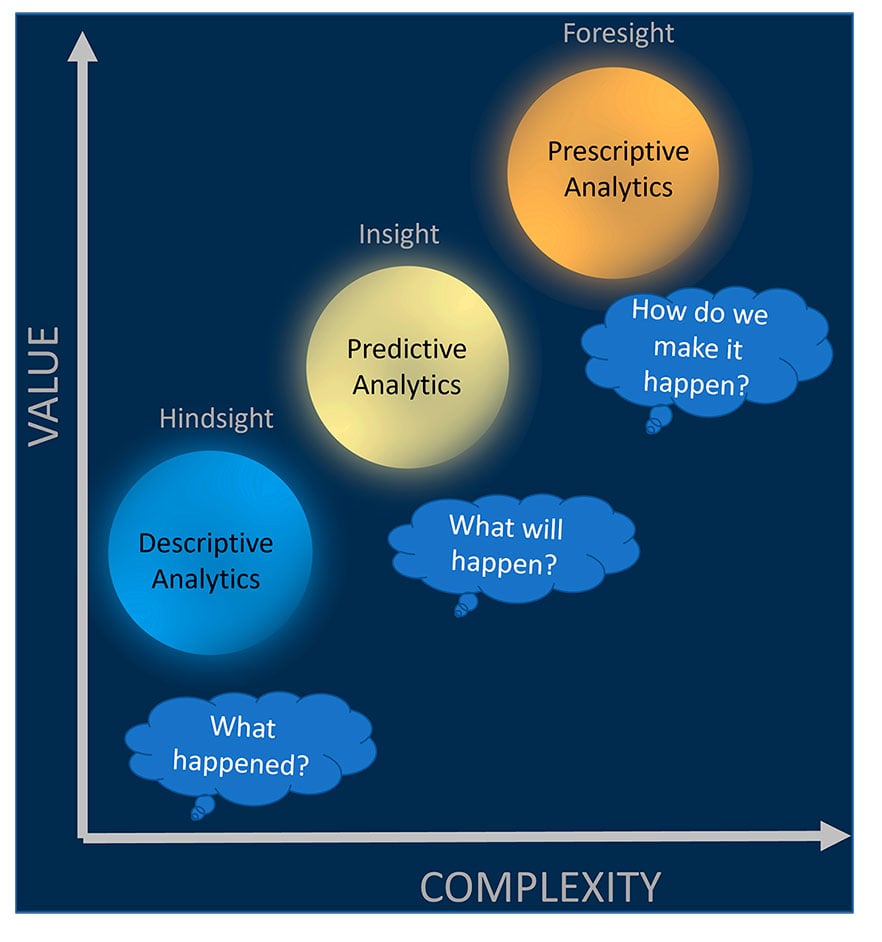
FIGURE 3: The Value Complexity Ramp of Analytics
Components and use cases
As well as providing decisions directly, extra value from MO comes from the explicit use of constraints. As introduced in last blog post, constraints are a good thing, and because of the way that MO works, unlike ML that is based on statistics, MO can ensure that constraints are honored in the resulting decisions.
In addition, an MO solution works with specific objectives, i.e. what we want to optimize. Whereas ML typically predicts one outcome, optimization typically seeks to balance more than one conflicting objective (as a simplification, consider the simultaneous objectives of maximizing revenue whilst minimizing spending on raw materials). FIGURE 4 shows the components of an MO solver in a workflow diagram.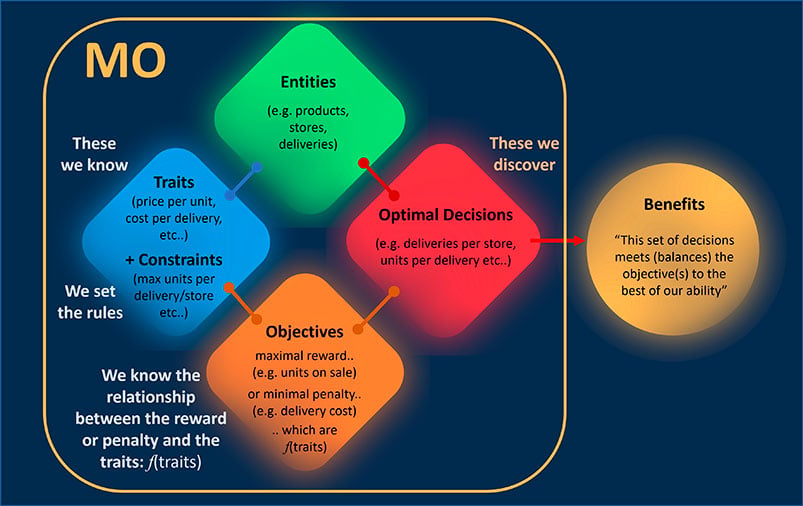
FIGURE 4: Components of a MO solver and its outcomes
Despite the favorable treatment of constraints and objectives, business and public entities have recently been less likely to adopt MO than ML. In a 2022 survey of organizations who use some form of data science for decision making, 75% use ML whereas only 24% use MO (the numbers for Finland are 72% & 24%).
These figures may reflect MO’s need for predetermined, factual relationships and data. When setting up an MO solver we need to know
- the relationship between decisions made and the objectives they affect
- the relationships between the objectives and the traits they depend on, a.k.a. “objective functions” f(traits)
- the values of the traits that the objectives depend on.
These requirements pose a bottleneck for MO that is already obvious in the Value Complexity Ramp (FIGURE 3). As the potential value of an analytics method increases so does the complexity created by requirements, which decreases the number of scenarios we can get it working for.
TABLE 2 summarizes the type of problem typically solved by MO and the characteristics of those problems that make MO a good candidate.
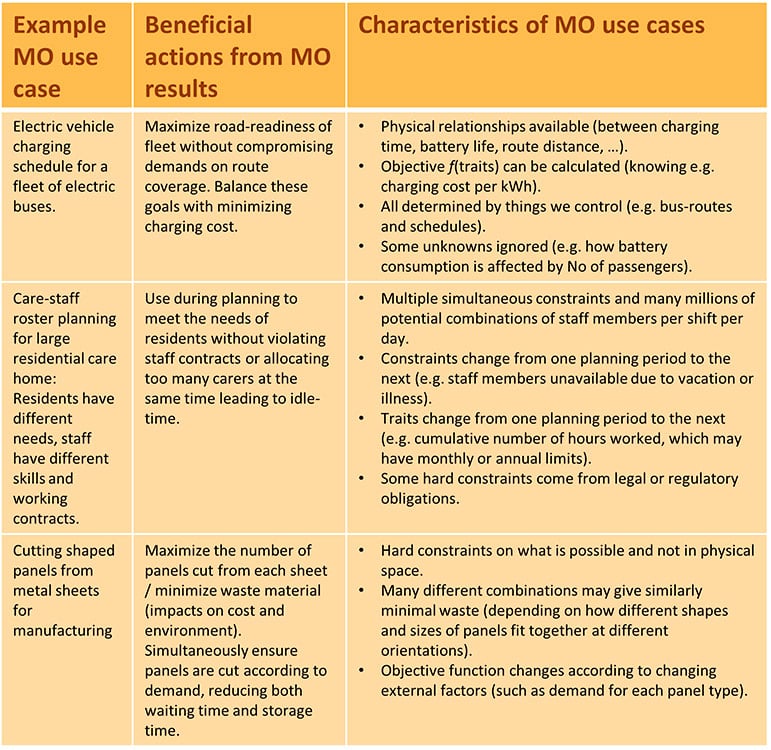
TABLE 2: Examples and characteristics of ML use cases.
To complete the comparison with ML, we note that just like an ML model, an MO solver should be considered a living thing. For ML we noted that models need to re-learn from fresh data to keep up with natural changes to facts and patterns on the ground. By introducing constraints and objectives, MO introduces more need for maintenance in order to
- adapt to changing constraints beyond our control,
- allow changes to business rules driven by strategy, and
- update the relationship between traits and objectives (e.g. changes to the retail price of units sold).
So where do we go from here?
Mathematical Optimization is a valuable tool that should appeal to business developers, controllers IT solution developers and professionals in many other roles who can start from a business problem and translate that into some objectives, constraints and a few ‘cause and effect’ relationships between possible decisions and probable outcomes. However, these ingredients of an MO solver can be hard to grab hold of and so just like ML, many use cases never see the light of day.
The good news is that the challenges to MO and ML are not the same. This gives us hope: can the two technologies solve each others’ problems?
In the next blog post in this series we will see how Mathematical Optimization can work together with Machine Learning together to address their respective bottle necks and provide a solution that offers a lot more value, through being applicable to a lot more use cases, without adding much extra complexity compared to using either technology on its own.
Can't wait? Download our whitepaper now to get access to the content right away.
