Koko valtakunta alkaa olla lumen peitossa, mikä auttaa huomattavasti Korvatunturilla asuvaa joulupukkia lahjojen toimittamisessa perille lyhintä mahdollista reittiä. Joulupukin reitin valinta lahjojen toimittamiseksi perille on tyypillinen kauppamatkustajan ongelma (traveling salesman problem, TSP), eli miten käydä useassa pisteessä vähintään kerran siten, että ajoreitti on mahdollisimman lyhyt.
Reki kiitää 188 kertaa maailman ympäri
Lyhimmän reitin löytäminen vajaan kahden miljoonan pisteen välille on haastava optimointiongelma.
Yleisesti ottaen, kun tarkastellaan n:ssä pisteessä käyviä reittejä, on eri reittivaihtoehtoja yhteensä (n-1)! kappaletta. Eli kun käyntipisteitä on n=2, 3, 4, 5, 6… löytyy vastaavasti reittivaihtoehtoja (n-1)! = 1, 2, 6, 24, 120…..
Normaalisti isot luvut näytetään kymmenen potensseina, joten muunnetaan tämä siihen muotoon:
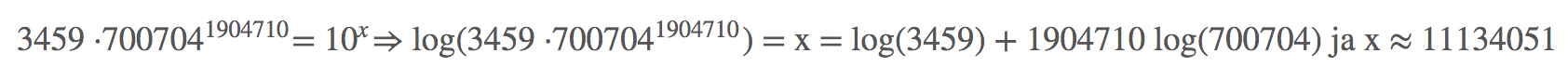
Voimme siis todeta, että pukilla on mahdollisia reittivaihtoehtoja reilusti yli 10¹⁰ ⁰⁰⁰ ⁰⁰⁰ kappaletta.
Kun havaittavassa maailmankaikkeudessa on noin 10⁸⁰ alkeishiukkasta, on hyvin ilmeistä, ettei ns. brute force -ratkaisulla päästä kovin pitkälle.
Reitti Korvatunturilta kaikkiin maailman asutuskeskuksiin ja takaisin on 7 515 756km pitkä, kun oletetaan, että pukki liikkuu Amerikan tyyliin lentävällä reellä.
Mikä on pukin optimaalisin reitti Suomen halki?
Samainen Kanadassa sijaitseva Waterloon yliopisto, jonka sivuilta löytyy maailman kaikissa kaupungeissa käyvä reitti, on koonnut listaa yksittäisten valtioiden kaikissa kaupungeissa käyvistä reiteistä. Sivuston mukaan Suomessa on 10 639 asutuskeskusta ja niiden välisen lyhimmän reitin pituus on 54 020km. Tämä on optimaalinen reitti, eli lyhin mahdollinen kaikista tarjolla olevista vaihtoehdoista.
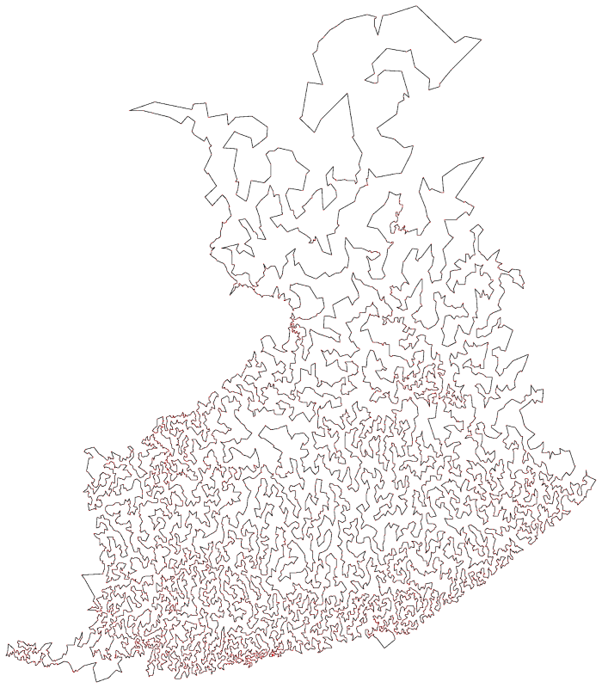
Ihan näin vähällä pukki ei kuitenkaan pääse pälkähästä. Asiakaspalautetta tulee taatusti jos lahjat jättää keskelle toria ja painelee suoraan seuraavaan paikkaan. Ainoastaan kotiovelle toimitus kelpaa jouluaattona, näin on aina ollut ja näin pitää aina olevan.
Kotitalouksien sijainneista on hankala löytää laadukasta aineistoa. Waterloon yliopisto on käyttänyt omissa laskennoissaan datalähteenä Yhdysvaltain puolustusministeriön alaista kuvatiedusteluaineistoa käsittelevää virastoa NGA:ta. NGA:lta saattaisi vaikka löytyäkin tarvittava aineisto, mutta siinä rikottaisiin jo niin monta GDPR-pykälää, että lienee turvallisempaa käyttää summittaista arviota.
Oletetaan, että jokainen asutuskeskus on yhden neliökilometrin kokoinen ja kotitaloudet ovat satunnaisesti jakautuneet alueelle. Yhden asutuskeskuksen kaikissa n:ssä kotitaloudessa käyvän lyhimmän polun pituus on Ln. Yllättävää kyllä, vielä ei tunneta mikä lyhimmän polun pituuden odotusarvo E(Ln) on! Mutta sille on kuitenkin olemassa ylä- ja alarajat. Wikipedian mukaan voimme olla lähes varmoja siitä, että odotusarvolle pätee:
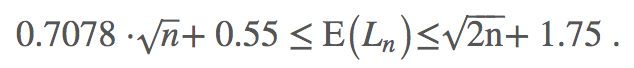
Näin ollen sadan kotitalouden kylän tapauksessa toimituksista ovelle asti aiheutuisi lisämatkaa noin 7.62-15.89km.
Omaan korvaan haarukka vaikuttaa turhan laajalta ja etenkin yläraja ihmetyttää. Lyhyt kirjallisuuskatsaus paljastaa, että yläraja on kohtalaisen korkealla kun vertaa laskennallisiin tutkimuksiin. Lisäksi Steinerbergerin (2014) mukaan teoreettiset rajat ovat myös selkeästi kapeammat:
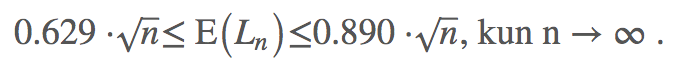
Suomessa on noin 100 000 asutettua neliökilometriä (100 338 kpl). Keskimääräinen kotitalouden koko on 2.02 henkeä, joten voimme jakaa jokaisen asutetun neliön väestön 2.02:lla ja saada tulokseksi kotitalouksien lukumäärän. Suuri osa maasta on hyvin harvaan asuttua ja teoreettiset rajat lyhimmän polun odotetulle pituudelle pätevät vain kun:
![]()
Käytetään siis laskennallisia tuloksia kun kotitalouksia on neliökilometrillä niukasti ja teoreettisia rajoja kun liikutaan tiheämmin asutulla alueella.
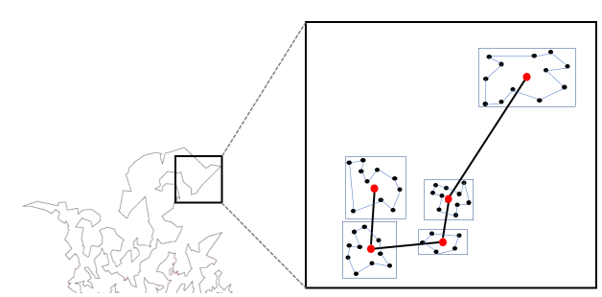
Kuva: Alkuperäisen reitin ja ovelle asti toimitusten yhdistäminen.
Pukilla on pitkä matka taivallettavana
Vielä yksi pieni pulma olisi ratkottava ennen kuin voidaan raportoida lopullinen lukema, sillä 100 338 asutettua neliökilometriä ja 10 639 käyntipistettä reitillä eivät ihan täsmää. Tarvitaan siis aimo annos käsien heiluttelua sovellettua matematiikkaa.
Yhteensä joulupukilla on siis noin 275 000km matka edessä, jotta kaikki suomalaiset saavat pakettinsa kotiovelle.
Perheissä on erilaisia perinteitä, mutta useimmat lahjat jaetaan klo 15–19. Tästä saamme joulupukin keskinopeudeksi 68 750km/h 19km/s. Ei ihan posketon lukema – jotkin avaruusluotaimet matkustavat jopa nopeammin.
Ei siis kannata ihmetellä, jos pukki vaikuttaa hieman hätäiseltä aattoiltana. Rommitotin tarjoaminen lämmikkeeksi kannattaa muuten varmuuden vuoksi jättää väliin. Jos joka kymmenennessä paikassa tarjotaan 2cl rommia, on pukki jo reilusti ennen reitin puoliväliä lähes 1000 promillen maistissa.
